Calcolo numerico

Aritmetica del calcolatore
- Sistemi non decimali
Numeri macchina
Stabilità di un algoritmo

Algebra lineare numerica

CONDIZIONAMENTO RELATIVO del problema Ax=b

Metodi per la soluzione di Ax = b

Metodi iterattivi per la soluzione di Ax=b

Soluzione di sistemi sovra-determinanti

Zeri di funzioni

Condizionamento delle radici di $f$
Criterio di arresto dello scarto (step)

Interpolazione dati e funzioni

Quadratura numerica

Missione: Costruire, algoritmi stabili per dati modelli matematici. Studiarne la convergenza sotto le ipotesi che i dati siano affetti da errore (di rappresentazione) e le operazioni siano svolte in aritmetica finita. Trovarne un’implementazione efficiente.

Programma

Aritmetica del calcolatore
Algebra lineare numerica
Calcolo di zeri e punti fissi
Interpolazione e approssimazione di dati e funzioni
Quadratura numerica

Matlab (Matrix Lab), linguaggio interpretato

Aritmetica del calcolatore

Sistemi non decimali

Sia $x\in\mathbb{R}\text{ e }N\in\mathbb{N_{0}}$ $x=\pm x_{n}N^{n}+x_{n-1}N^{n-1}+…+x_0+x_{-1}N^{-1}+…+x_{-r}N^{-r}=:(x)_{N}$ dove $N$ base

Conversione da base N a base M $\begin{align*}x&=x_{n}N^{n}+x_{n-1}N^{n-1}+…+x_{0}x_{-1}N^{-1}+…+x_{-r}N^{-r}\\&=y_{m}M^{m}+y_{m-1}M^{m-1}+…+y_0+y_{-1}M^{-1}+…+y_{-q}M^{-q}\end{align*}$

Per la parte intera divisioni $(x_\text{int})_{N}$ per $M$ $y_{0}= (\mod x,M)$ $y_{1}=(\mod q_{0},M)$ $\vdots$ $y_{m}=(\mod q_{m},M)$ Per la parte frazionaria moltiplicazioni $(x_\text{fraz})_{N}$ per $M$ $y_{-1}=q_{-1}\cdot M$

Numeri macchina

IEEE 754

integer
real (floating point)

Interi macchina: $\pm (x)_{2}$

Floating point

| N bit | $\pm$ | Esponente | Parte intera + Parte frazionaria | | —— | —– | ——————— | ——————————– | | | 0/1 | $((2^{k-1}-1)-e)_{2}$ | | | 32 bit | 1 bit | 8 bit | 23 bit | | 64 bit | 1 bit | 11 bit | 52 bit | Nello standard IEEE 754

0 è rappresentato con $e=0, f=0$
$+\infty$ è rappresentato con $e=255, s=0, f=0$
$-\infty$ è rappresentato con $e=255, s=1, f=0$
NaN è rappresentato con $e=255, f>0$

Es. $(12345.125){10}$in IEEE 754 a 32bit Segno +=0 Parte intera$(12345){10}=(11000000111001){2}$Parte frazionaria$(0.125){10}=(.001){2}$Esponente bias 127+13=$(140){2}=(10001100)_{2}$$

0 10001100 1000000111001

Massimo modulo rappresentabile

\[\displaystyle1.f=1.\underbrace{1111…}_{23}=\sum_{k=0}^{-23}2^{k}=\sum_{k=0}^{23}\left(\frac{1}{2}\right)^{k}=\]
$e=$ massimo possibile $\displaystyle=11111111=\sum_{k=0}^{7}2^{k}=\frac{1-2^{8}}{1-2}=2^{8}-1=255$ Minimo modulo rappresentabile
\[1.f=1.\underbrace{0000…}_{23}\]
$e=0-127=-127$ $1.f\cdot2^{e-b}=2^{-127}$

Spaziatura dei numeri in $\mathbb{F}_{32}$ se $k\in\mathbb{F}_{32},\ |x|\neq M_{max},\ x\neq0$ è ben definito al precedente `prec(x)` e il successivo `succ(x)` $|x-succ(x)|=?$ per semplicità $x>0$ $x=1.f\cdot2^{e-b}\qquad x+00…01\cdot2^{e-b}=succ(x)$ $|x-succ(x)|=2^{e-b-23}$ dove $e$ è quello di $x$

$x-00…01\cdot2^{e-b}=prec(x)\qquad|x-prec(x)|=2^{e-b-23}$ $\begin{align*}d: \mathbb{F}&\longrightarrow\mathbb{R}_{\geq}\\ x&\longmapsto\text{distanza tra }\mathbb{T}_{32}\end{align*}$

Il sistema ha una qualità di rappresentazione RELATIVA (al $$

$) che è COSTANTE viceversa possiamo dire che la spaziatura varia PROPORZIONALMENTE a$

Quando ci sono cifre in più possiamo

$fp^{Tr}$ Troncamento, le cifre non vengono considerate $fp^{Tr}(x)=\begin{cases}-M_{max}&\forall x\leq-M_{max}\\ \text{rappresentazione troncata di }x&x\in]-M_{max},M_{max}[\\M_{max}&\forall x\geq M_{max}\end{cases}$
$fp^{Ar}$ Arrotondamento (standard), l’ultima cifra è memorizzata il numero successivo se la cifra seguente è 1 il numero precedente se la cifra seguente è 0

Def. Se $\tilde{x}\in\mathbb{R}$ è pensata come approssimazione di $x\in\mathbb{R}$ allora “ERRORE ASSOLUTO DI $\tilde{x}$” è $err_{ASS}(\tilde{x}):=|x-\tilde{x}|$e ERRORE RELATIVO DI $\tilde{x}$ è$err_{REL}(\tilde{x}):=\frac{|x-\tilde{x}|}{|x|}\qquad \text{se }x\neq0$

Osservazione: Se abbiamo $x\in\mathbb{R}^{n}$ fissiamo una norma $\|\cdot\|$ se $\mathbb{R}^{n}$ $err_{ASS}(\tilde{x}):=\|x-\tilde{x}\|$ $\displaystyle err_{REL}(\tilde{x}):=\frac{\|x-\tilde{x}\|}{\|x\|}\qquad\text{se }\|x\|\neq0$

Errore di Rappresentazione ERRORE ASSOLUTO DI RAPPRESENTAZIONE di $x$ con $fl^{Tr/Ar}$$err_{ASS}(fp^{Tr/Ar}(x))=|x-fp^{Tr/Ar}(x)|$ ERRORE RELATIVO DI RAPPRESENTAZIONE di $x$ con $fl^{Tr/Ar}$$err_{REL}(fl^{Tr/Ar}(x))=\frac{|x-fl^{Tr/Ar}(x)|}{|x|}\qquad\forall x\neq0$ Stimare l’errore di rappresentazione.

Troncamento $(fp\rightarrow fp^{Tr})$ $|fp(x)-x|\leq?$ Supponiamo $x>0$ $|fp(x)-x|\leq|fp(x)-succ(fp(x))|=d(fp(x))$ $=2^{e(x)-b}\cdot2^{-n_{f}}$ $err_{ASS}(fp^{Tr}(x))\leq2^{-n_{f}}2^{e(x)-b}$ $err_{REL}(fp^{Tr}(x))\leq\frac{2^{n_{f}}2^{e(x)-b}}{|x|}\leq 2^{-n_{f}}\centernot{\frac{2^{e(x)-b}}{2^{e(x)-b}}}$
Arrontondamento $(fp\rightarrow fp^{Ar})$ $|x-fp(x)|\leq\frac{|fp(x)-prec(fp(x))|}{2}$ $err_{REL}(fp^{Ar}(x))\leq\frac{2^{-n_{f}}}{2}=2^-(n_{f}+1)$

Nomenclatura: Si dice PRECISIONE DI MACCHINA, il più piccolo numero $fp$ positivo $\epsilon_{MACH}$ per cui $1+\epsilon_{MACH}\neq1$ Per noi $\epsilon_{MACH}=2^{-n_{f}}$

Operazione Macchina Per ogni operazione reale $\ast$ resta associata una operazione MACCHINA (che denotiamo come $\circledast$) definita come $x\circledast y:=fl(fl(x)\ast fl(y))$Attenzione alle parentesi! Il risultato SPACCA L’ALGEBRA ELEMENTARE.

Cose da non fare

non è commutativa
non è associativa
non distribuisce rispetto a $\oplus$
gli elementi neutri di $\oplus\text{ e }\odot$ non sono unici
non vale la proprietà di cancellazione

Esempio $1\oplus1/8=9/8$ $\begin{align}1=(1.0)_{2}\cdot2^{0}\qquad&1.0000+\1/8=(1.0)_{2}\cdot2^{3}\qquad&0.0010=\\qquad&1.0010\cdot2^0=9/8\end{align}$$

$8\oplus1/8=8$ $$\begin{align}8=(1.0)_{2}\cdot2^{3}\qquad&1.000000+\\qquad&0.000001=\ &1.0000|01=1.0000\cdot2^3=8\end{align}$

Stabilità di un algoritmo

Un algoritmo si dice STABILE se “non amplifica in modo incontrollato gli errori presenti sui dati”. Vogliamo una STIMA DI STABILITÀ.$err_{rel}(output)\leq C_{STAB}\ err_{rel}(input)$ Stima della stabilità della somma (algebrica) $x\oplus y=fl(fl(x)+fl(y))$ $\displaystyle=\frac{|x\oplus y-(x+y)|}{|x+y|}\leq\ ?\qquad$ chiamo $fl(x)+fl(y)=:z$ \(\begin{align*}=&\frac{|fl(z)-x-y|}{|x+y|}=\frac{|fl(z)-z+z-x-y|}{|x+y|}=\\&\frac{|fl(z)-z+fl(x)-x+fl(y)-y|}{|x+y|}\\\leq&\frac{|fl(z)-z|+|fl(x)-x|+|fl(y)-y|}{|x+y|}=\\ &\underbrace{\frac{|fl(z)-z|}{|z|}}\frac{|z|}{|x+y|}+\underbrace{\frac{|fl(x)-x|}{|x|}}\frac{|x|}{|x+y|}+\underbrace{\frac{|fl(y)-y|}{|y|}}\frac{|y|}{|x+y|}\\&\}\rightarrow\text{dominati da }\varepsilon_{MACH}(o\ \frac{\varepsilon_{MACH}}{2})\\\leq&\varepsilon_{MACH}\left[\frac{|z|}{|x+y|}+\frac{|x|+|y|}{|x+y|}\right]=\\&\varepsilon_{MACH}\left[\frac{|fl(x)+fl(y)|}{|x+y|}+\frac{|x|+|y|}{|x+y|}\right]=\\&\varepsilon_{MACH}\left[\frac{|fl(x)-x+x+fl(y)-y+y|}{|x+y|}+\frac{|x|+|y|}{|x+y|}\right]\\\leq&\varepsilon_{MACH}\left[\frac{|fl(x)-x|+|x+y|+|fl(y)-y|}{|x+y|}+\frac{|x|+|y|}{|x+y|}\right]=\\&\varepsilon_{MACH}\left[\underbrace{\frac{fl(x)-x}{|x|}}\frac{|x|}{|x+y|}+1+\underbrace{\frac{fl(y)-y}{|y|}}\frac{|y|}{|x+y|}+\frac{|x|+|y|}{|x+y|}\right]\\\leq&\varepsilon_{MACH}\left[\varepsilon_{MACH}\frac{|x|+|y|}{|x+y|}+1+\frac{|x|+|y|}{|x+y|}\right]=\\&\frac{|x|+|y|}{|x+y|}\varepsilon_{MACH}(\varepsilon_{MACH}+1)+\varepsilon_{MACH}\end{align*}\)

$\displaystyle err_{rel}(x\oplus y)\quad\leq\quad\varepsilon_{MACH}+\varepsilon_{MACH}(\varepsilon_{MACH}+1)\underbrace{\frac{|x|+|y|}{|x+y|}}_{g(x,y)}\blacktriangle$ PROBLEMA: quando $x\approx -y$

In questo esempio la disuguaglianza $\blacktriangle$ si dice $err_{REL}(x\oplus y)\leq 1+\varepsilon_{MACH}$ cioè un ERRORE RELATIVO DI + DEL 100% Quando ciò accade si parla di CANCELLAZIONE NUMERICA.

xcasa: Calcolare l’errore relativo $1\oplus(-1-1^{-k})$ con $k=n_{f},n_{f}+1,…$

Esempio di Instabilità $\displaystyle I_{n}=\frac{1}{e}\int_{0}^{1}x^{n}e^{n}dx\qquad$ si dimostra che $I_{n}\rightarrow 0$ $\begin{cases}I_{n}=1-nI_{n-1}\\ I_{n}=\frac{e-1}{e}\end{cases}$ $\begin{align*}\tilde{I}_{n}=&I_{n}-\varepsilon_{n-1}\\=&1-n\tilde{I}_{n-1}=1-n(I_{n-1}+\varepsilon_{n-1})\\=&1-\end{align*}$

Flusso di lavoro / Pensiero del C. N. $\begin{array}{ccc}\boxed{\text{Real world problems}}\dashrightarrow&\boxed{\text{Problema matematico}}\\ &\downarrow\\&\boxed{\text{Schema numerico}}\longrightarrow&\boxed{\text{Algoritmo}}\rightarrow\boxed{\text{SW}}\end{array}$

Problemi matematici che affronteremo saranno della forma (Trovare $x\in {X_{DOMINIO}}:F(n,d)=0\qquad d\in D_\text{DATI AMMISSIBILI}$)

Problemi BEN POSTI

Definizione del DOMINIO e dei DATI AMMISSIBILI
\[\forall d\in D,\qquad\exists!\ x\in X:F(n,d)=0\]
$d\mapsto x(d)$ soluzione del problema (mappa soluzione) è CONTINUA

”zona grigia” Problemi INVERSI non sono esattamente ben posti ma vengono comunque affrontati con tecniche che li riconducono a problemi simili ma ben posti.

Sono ben posti?

Trovare $x\in\mathbb{R}^n$ tale che $Ax=b$ com $A\in\mathbb{R}^{n\times m}b\in\mathbb{R}^n$ $\displaystyle\begin{bmatrix}0&0\\0&0\end{bmatrix}x=\left[{1\atop1}\right],x\text{ non esiste}\qquad\text{ e }\qquad\begin{bmatrix}0&0\\0&0\end{bmatrix}x=\left[{0\atop0}\right],x\text{ qualunque}$ Non è ben posto.

CONDIZIONAMENTO ASSOLUTO di un problema matematico Un problema si dice BEN CONDIZIONATO se a piccole variazioni dei dati corrisponde piccole variazioni della soluzione. LOCALE$\limsup_{\tilde{d}\rightarrow d}=\frac{|x(\bar{d})-x(d)|}{|\bar{d}-d|^{\alpha}}\leq k_{\alpha}(d)\qquad0<\alpha\leq1$GLOBALE (di ordine $\alpha$) in D$\sup_{d\in D}k_{\alpha}(d)\leq k_{\alpha}<+\infty$Osservazione: Il buon condizionamento è una proprietà del PROBLEMA, NON DEL METODO DI SOLUZIONE. In particolare esistono algoritmi stabili per problemi mal condizionati e algoritmi non stabili per problemi ben condizionati. Noi useremo quasi sempre la versione con $\alpha=1$.

Osservazione: dalla definizione $k_{\alpha}(d)$ è noto allora esiste un intorno $I$ di D tale che

CONDIZIONAMENTO RELATIVO$\limsup_{\tilde{d}\rightarrow d}\frac{|x(\tilde{d})-x(d)|}{x(d)}\left(\frac{|d|}{|\tilde{d}-d|}\right)=k_{\alpha}^{rel}(d)$GLOBALE$\sup_{d\in D}k_{\alpha}^{rel}(d)=:k_{\alpha}^{rel}$Problema: Trovare $x\in X:\ F(x,d)=,d\in D$ Metodo ammesso: Trovare $x_{n}\in X_{n}:F_{n}(x,d)=,d\in D$ $\alpha\in\mathbb{N}\text{ e }X_{n},F_{n}$ “approssimano” $X,F$ in senso opportuno. Si vorrebbe che (c) $\rightarrow x(d)\text{ se }\text{ per ogni }d\in D$ (c) prende il nome di CONVERGENZA del METODO (c.v) convergere se si divide per $\sup_{d\in D}|x_{n}(d)-x(d)|=0$

Def. Il metodo $x\in X_{n}:F_{n}(x_{n},d)=0\text{ per }d\in D$ e si dice CONSISTENTE se$\lim_{n\rightarrow+\infty}F_{n}(x(d), d)=0$Teorema (LAX-RICHMEYZA) Se un metodo è CONSISTENTE allora è

CONVERGENTE $\Longleftrightarrow$ è STABILE
Algebra lineare numerica

$Ax=b$ è ben posto se $A\in M_{n\times n}$ INVERTIBILE e $b\in\mathbb{R}^{n}$ soluzione è $x=A^{T}b$ $n$ potrebbe essere $>>1$

Norme compatibili (indotte) di matrici Sia $\|\cdot\|:\mathbb{R}^{n}\rightarrow\mathbb{R}_{>0}$ una norma

\[\|x\|\geq x\text{ e }\|x\|\leq x\rightarrow x=0\]
$\|dx\|=|d|\|x\|$
Osservazione: ogni volta che scelto una norma su $\mathbb{R}^{n}$ viene definita una norma indotta sulle matrici $M_{n\times n}(\mathbb{R})$ Sia $\begin{align}\|\cdot\|_{*}:&M_{n\times n}(\mathbb{R})\rightarrow\mathbb{R}_{\geq0}\\ &A\longmapsto\sup_{x\neq0}\frac{\|Ax\|}{\|x\|}\end{align}$ Proposizione: $\|\cdot\|_{*}$ è una norma $\|A\|_{*}=\sup_{\|x\|=1}\|Ax\|$

CONDIZIONAMENTO RELATIVO del problema Ax=b

Per il momento considero il dato ($D=\mathbb{R}^{n}$) ed $A$ fissata e rappresentata osatamente. $\tilde{b}\simeq b,\ A\tilde{x}=\tilde{b}$ $\tilde{b}=b+\delta b\qquad\tilde{x}=x+\delta x$ $A(x+\delta x)=b+\delta b$ voglio stimare l’errore relativo $\dfrac{\|\delta x\|}{\|x\|}$ $\begin{rcases}A()=\\ Ax=b\end{rcases}\rightarrow A\tilde{}x=b-Ax$

Osservazione: $\boxed{\begin{align}\|A\|_{*}=\sup_{}\frac{\|\|}{\|\|}\geq\frac{A}{\|\|}\\\Longrightarrow\|A\tilde{x}\|\leq\|A\|_{*}\|\tilde{x}\|\end{align}}$

questo stima il CONDIZIONAMENTO ASSOLUTO. (*)$\|\delta x\|=\|A^{-1}\delta b\|\leq\|A^{-1}\|_{*}\|\delta b\|$

$\dfrac{err_{rel}(x)}{err_{rel}(b)}\leq\|A^{-1}\|_{*}\|A\|_{*}$ CONDIZIONAMENTO RELATIVO GLOBALE $\|b\|=\|Ax\|\leq\|A\|_{*}\|x\|\Rightarrow\|x\|\geq\frac{\|b\|}{\|A\|_{*}}$ $\frac{\|\delta x\|}{\|x\|}\leq\frac{\|\delta x\|}{\|b\|}\|A\|_{*}\leq\underbrace{\|A^{-1}\|_{*}\|A\|}_{Cond(A,\|\cdot\|_{\geq1})}\frac{\|\delta b\|}{\|b\|}$ Per questa ragione la quantità $\|A^{-1}\|\|A\|_*$ merita un nome di “numero di condizionamento di A con norma $\|\cdot\|_{*}$”

Possiamo perdere molta precisione
La stima che abbiamo ottenuto è una worst-case analysis

Caso generale A,b sono “dati” (potrei rappresentare A con errore) $(A+\delta A)(x+\delta x)=b+\delta b$ $(A+\delta A)\delta x=\cancel{b}+\delta b-\cancel{Ax}-\delta Ax$ $A(\mathbb{1}+A^{-1}\delta A)\delta x=\delta b-\delta Ax$ $(\mathbb{1}+A^{-1}\delta A)\delta x=A$

SERIE DI NEUMANN Inversione di matrice definita come serie. $\frac{1}{1+x}=1$ $B^{k}=P^{-1}\wedge P$ $\begin{align*}\mathbb{1}+B=&\mathbb{1}+P^{-1}\wedge P=P^{-1}P+P^{-1}\wedge P\\=&\end{align*}$ Per B quadrata diagonalizzabile con $|\lambda_{B}|<1$ si ha $()$

Osservazione: Si può dimostrare che che $\forall B,\varepsilon>0$ $\exists B$ diagonalizzabile con $\|B-B_{2}\|<\varepsilon$

È usabile con $1+A^{-1}\delta A=1+A^{-1}\|A\|_{*}\frac{\delta A}{\|A\|_{*}}=1+(\frac{A}{})^-1$ Se $B=(\frac{A}{})^{-1}\frac{\delta A}{}$ $\underset{\text{sub-multiplicatività}\atop\text{matrici indotte}}{<}\|(\frac{A}{})^{-1}\|$

Metodi per la soluzione di Ax = b

Metodi diretti che costituiscono la soluzione numerica (componente per componente) e di norma si possono tradurre in FATTORIZZAZIONI DI MATRICI $A=B\cdot C$.

Metodi iterattivi costruiscono una successione (di vettori) di approssimazioni della soluzione. Tipicamente come $x^{o}=\text{dato}\qquad$ $x^{k+1}=Ex^{k}+q$

Supponiamo che A sia o $\begin{align*}\nearrow&\text{ triangolare superiore}\\\searrow&\text{ triangolare inferiore}\end{align*}$

Input A, b, n
X(n) = b(n)/A(n,m)
for k=1 to n-1
	X(n-k) = (n(n-k)-cumsum(A(n-k,n-k+j)*X(n-k+j),j=1,k))/A(n-k,m-k)

xcasa: scrivere codice per triangolare inferiore.

FATTORIZZAZIONE L.U. (metodo diretto) La riduzione Gaussiana si può scrivere come fattorizzazione $A=LU\qquad\text{dove }\begin{cases}L\text{ triangolare inferiore}\\ U\text{ triangolare superiore}\end{cases}$$Ax=b\quad\Longleftrightarrow\quad LUx=b$se chiamo$Ux=y$ho$Ly=b$$ ALGORITMO SOSTITUZIONE IN AVANTI MI DA

Possiamo ricondurci al caso triangolare? $\left[\begin{array}{c|cc}a_{11}&\ &\ \\\vdots&\ &\ \end{array}\right]$ Voglio annullare i numeri nella prima colonna tranne $a_{11}$ Uso moltiplicatori.$\tilde{L}^{(1)}=\begin{cases}A^{0}=A\ A^{k+1}=I^{(k)}A^{(k)}\end{cases}\qquad I^{(k)}=\mathbb{1}-\begin{pmatrix}0\\vdots\0\\frac{a^{(k)}{1,k}}{a^{(k)}{k,k}}\\vdots\\frac{a^{(k)}{n,k}}{a^{(k)}{k,k}}\end{pmatrix}e_{k}^{T}v$vettore colonna$u$vettore riga$(vk^{T}){ij}=v{i}u_{j}\Rightarrow$in particolare$v\cdot e_{k}^{T}=\left[\begin{array}{ccc|c|ccc}0&…&0&&0&…&0\\vdots&&\vdots&v&\vdots&&\vdots\0&…&0&&0&…&0\end{array}\right](AB)$Alla fine degli n-1 passi abbiamo calcolato$A^{1},A^{2},…,A^{n-1}\qquad \tilde{L}^{1},\tilde{L}^{2},…,\tilde{L}^{n-1}\in M_{n\times m}\begin{align}A^{0}&=A\ A^{1}&=\tilde{L}^{1}A\ A^{2}&=\tilde{L}^{1}A^{1}=\tilde{L}^{1}\tilde{L}^{2}A\&\vdots\ U:=A^{n-1}&=\tilde{L}^{(n-1)}…\tilde{L}^{(1)}A\end{align}$$

Avevo detto che avremo ottenuto $A=LU$ Se $(I^{n-1}…I^{1})$ è invertibile, allora $(I^{n-1}…I^{1})^{-1}U=A$ $I^{(k)}$ è invertibile?? Se sì, allora $(I^{n-1}…I^{1})^{-1}=(I^{1})^{-1}…(I^{n-1})^{-1}=:L$ Definiamo $(L^{(k)})_{i,j}=\begin{cases}\tilde{L}^{(k)}_{i,j}&\text{se }j\geq i\\-\tilde{L}^{(k)}_{i,j}&\text{se }j<i\end{cases}$ e dimostriamo che $L^{(k)}=(\tilde{L}^{k})^{-1}$ $\tilde{L}^{(k)}=\mathbb{1}-\begin{pmatrix}0\\\vdots\\0\\1\\ v^{(k)}\end{pmatrix}e_{k}^{T}=\begin{pmatrix}1&0&…&…&0\\0&1&0&…&0\\0&0&1&0&…\\&0&(v^{(k)})&\mathbb{1}_{n-j}\end{pmatrix}$

Da notare che è possibile arrivare ad ottenere un pivot 0.

IDEA: “Pivot parziale” Se scambio le righe di A posso ottenere che l’elemento in posizione di pivot sia il massimo modulo dalla parte della colonna a disposizione cioè $|a_{kk}^{k}|=\max\{\}$

SCAMBIARE LE RIGHE VUOL DIRE SCAMBIARE L’ORDINE DELLE EQ -> SIST. EQ (se scambio anche il termine noto)
Teorema: Se A è invertibile, allora effettuando il pivoting parziale (per righe) otterrò sempre $a_{kk}^{k}\neq0\quad\forall\ k=1,2,…,n-1$
IL PIVOTING PARZIALE STABILIZZA L’ALGORITMO LU -evitando gli errori di cancellazione numerica -evitando le divisioni per numeri molto piccoli

Algoritmo LU con PIVOT PARZIALE per righe $P^{k}=$ matrice $n\times m$ di permutazione che scambia la riga k-esima con l’i-esima dove l’ ”i” è quello che verifica $(*)$

$P^{k}$ è dunque $\mathbb{1}$ con la riga i e k scambiate Se P è matrice di permutazione $P^{T}P=\mathbb{1}$ dunque P è matrice ortogonale, in particolare $P^{T}=P^{-1}$.

$\tilde{A}^{k}=P^{k}A$ Qui faccio un passo di LU senza PIVOTING cioè calcolo $\tilde{L}^{k}$ partendo da $\tilde{A}^{k}$ invece che da $A^{k}$ $\tilde{L}^{k}\tilde{A}^{k}=P^{k}A$ $\begin{align*}A\\ P^{1}A&=\tilde{A}^{1}\\\tilde{L}^{1}P^{1}A&=\tilde{A}^{2}\\P^{2}\tilde{A}^{2}&=P^{2}\tilde{L}^{1}P^{1}A\\&\vdots\\\end{align*}$ $P^{n-1}\tilde{L}^{n-1}P^{n-2}\tilde{L}^{n-2}…\tilde{L}^{1}P^{1}A=\tilde{A}^{n-1}=:U$

\[\boxed{PA=LU}\]

Volevo risolvere $Ax=b\quad\rightarrow\quad PAx=Pb$ $\Leftrightarrow\qquad LUx=Pb\quad$con SOST. AVANTI E SOS. INDIETRO

Metodi iterattivi per la soluzione di Ax=b

IDEA: Creare in modo ”economico” una soluzione $x^{(k)}\in\mathbb{R}^n\quad\forall k\in\mathbb{N}$ che approssima x soluzione. Motivazione: Il metodo diretto impiega molto tempo per matrici grandi. Un metodo diretto non calcola comunque la soluzione esatta a causa degli errori di rappresentazione e della loro propagazione.

Un generico metodo iterattivo $x^{o}=$ dato $x^{(k)}=F(x^{k})\quad\forall\ k=1,…$ Metodi iterattivi stazionari lineari $x^{o}=$ dato $x^{(k)}=Ex^{k}+q,\qquad E\in M_{n\times m}(\mathbb{R}),q\in\mathbb{R}^{n}$ Vogliamo che $x^{k}\underset{x}{\longrightarrow}$

Generalmente un metodo iterattivo si studia utilizzando il concetto di PUNTO FISSO. Det: $F:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}$

Se $x^{k}\longrightarrow\bar{x}$ allora, se $F$ è continua, anche k il metodo converge ASINTOTICAMENTE. $\displaystyle\bar{x}:=\lim_{k\rightarrow+\infty}x^{*}$ è PUNTO FISSO. Quindi voglio creare F in modo che se $x^{*}$ è P. FISSO di F allora è soluzione di Ax = b. se $x^{*}$ è P. FISSO $\qquad x^{*}=F(x^{k})=Ex^{*}+q$ se $x^{*}$ è sol. di $Ax = b\qquad x^{*}=A^{-1}b$ dunque $(\mathbb{1}-E)A^{-1}b=q$

Dati $E,q,x^{*}$ quando succede che $x^{*}$ è SUCC. CONTINUA? LEMMA DELLE CONTRAZIONI (caso $F:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}$) Sia $F:\mathbb{R}^{n}\rightarrow\mathbb{R}^{n}\text{ e }L<1$ tale che$\forall\ x,y\in\mathbb{R}^{n}\quad\|F(x)-F(y)\|\leq\ell\|x-y\|$($\|\cdot\|$ è una qualsiasi norma) Allora per $x^{*}\in\mathbb{R}^{n}$ la successione

SUCCESSIONE DI CAUCHY

Completezza di $\mathbb{R}^{n},\|\cdot\|$ Una successione $x^{k}\in\mathbb{R}^{n}$ è completa SE E SOLO SE è di Cauchy.

$x^{k}$ è SUCC. DI CAUCHY e dunque HA LIMITE in $\mathbb{R}^{n}$. Mostriamo che $x^{k}\longrightarrow x^{*}$ PUNTO FISSO$\begin{align*}x^{k+1}=F(x^{k})<\|F(x)-F(y)\|\leq L\|x-y\|\end{align*}$Mostriamo stima sull’errore $e_{k+1}=\|x^{k+1}-x^{*}\|=\|F(x^{k})-F(x^{*})\|\leq L\|x-y\|$

Condizione necessaria purché il punto fisso di F sia soluzione Ax = b Sia soluzione di Ax = b

()

PRIMA SCELTA SENSATA $\begin{rcases}E=\mathbb{1}-A\\ q=b\end{rcases}\rightarrow$ definiscono il metodo di Richardson $\begin{cases}x^{o}=\text{dato}\\ x^{k+1}=(\mathbb{1}-A)x^{k}+b\end{cases}$

Valgono le ipotesi del lemma?? $\begin{align*}\|F(x)-F(y)\|=\|(\mathbb{1}-A)x+q-[(\mathbb{1}-A)y+q]\|=\\\|(\mathbb{1}-A)(x-y)\|\leq\|\mathbb{1}-A\|_{*}\|x-y\|=\|E\|_{*}\|x-y\|\end{align*}$ $\leq\ \leftarrow\|A\|_{*}:=\sup_{x\neq0}\frac{\|Ax\|}{\|x\|}$

$\|F(x)-F(y)\|\leq\|E\|_{*}\|x-y\|\quad\forall x,y$ dunque prendo $L:=\|E\|_{*}$ e voglio L < 1 questa disuguaglianza dipende da CHE norma uso.

Possiamo capire meglio il funzionamento del metodo guardando le proprietà SPETTRALI di E. $x^{o}$ $x^{1}=Ex^{*}+q$ $x^{2}=Ex^{1}+q=E(Ex^{0}+q)+q=E^{2}x^{0}+Eq+q$ $x^{3}=Ex^{3}+q=$ $x^{k}=E^{k}x^{o}+\sum\limits_{j=0}^{k-1}E^{j}q\qquad E^{k}=\overbrace{E\cdot E…E}$

Cosa $A=P\Lambda P^{-1}$ $\begin{align*}A=P^{-1}\text{diag}(\frac{1}{\lambda_{i}})P&=P^{-1}\Lambda PP^{-1}\Lambda^{-1}P=P^{-1}\Lambda\Lambda^{-1}P\\&=P^{-1}P=\mathbb{1}\end{align*}$ quindi $\displaystyle\lim_{x\rightarrow+\infty}x^{k}=A^{-1}b=x^{x}$

Dunque basta che $|1-\lambda_{i}|<1\quad\forall\ i$ e che A sia diagonalizzabile. $\Rightarrow$ Richardson converge!

Si può mostrare che PROP: Se $p(E)<1$, allora $x^{k+1}$

Se P è una matrice invertibile “facile” allora $P^{-1}(b-Ax)+x=x$

Il metodo di Richardson Predicondizionato $P^{-1}b+P^{-1}Ax^{x}+x^{0}=x$ $\begin{cases}x^{0}\\ P^{-1}b+(\mathbb{1})\end{cases}$

Metodi di “Jacobi” e “Gauss-Seidel” $A=\underset{\text{triang inf}}{L}+\underset{\text{diag}}{b}+\underset{\text{triang sup}}{U}$ JACOBI: faccio metodo di Richardson Precondizionato con P=D $D^{-1}Ax=D^{-1}b$ è posso fare $p(E)=\max\{ d\}$ In Perché? Lemma dei cerchi di Gershgorin Gli auto valori si trovano in una combinazioni di cerchi con centro

GAUSS-SEIDEL: $P=L+D$ $P^{-1}b-P^{-1}Ax^{k}+x^{k}=x^{k+1}$ $P^{-1}b-P^{-1}(P+U)+x^{k}=x^{k+1}$ $P^{-1}b-P^{-1}Ux^{k}+x^{k}=x^{k+1}$ $\xLeftrightarrow{\text{equivale a fare}}$ $Px^{k+1}=b-Ux^{k}$ risolto per sostituzione indietro $E=P^{-1}U$ $q=P^{-1}b$ Tipicamente performa meglio di Jacobi ma è più difficile trovare condizioni per convergenza…

TUTTI I METODI ITERATTIVI VISTI PER DIVENTARE ALGORITMI HANNO BISOGNO DI UN CRITERIO DI ARRESTO.

Possibile criterio “residuo relativo piccolo” residuo di un sistema lineare $\neq$ errore! $Ax-b\ ,\ \|Ax-b\|$ Ad esempio mi posso fermare quando $\|Ax^{k}-b\|<\text{toll}$ ma, se uso $Axb$ con $kA\text{ e }kb$ l’errore cresce Allora si usa$err_{rel}\frac{\|Ax^{k}-b\|}{\|b\|}<\text{toll}$$\begin{align}err_k&=|x^-x^k|=|A^{-1}A(x^-x^k)|\leq|A^{-1}|_|A(x^x^k)|\&=|A^{-1}|_|b-Ax^k|=|A|err\end{align*}$$

quindi se mi fermo quando residuo è minore alla tolleranza $res^{REL}_{k}<\text{Toll}$, ho errore relativo minore del condizionamento della norma $err^{REL}_{k}<\text{Cond}(A)\cdot\text{Toll}$ Un’altra strategia è quella dello “SCARTO” (STEP). In un metodo interattivo${x^{k}}_{k\in\mathbb{N}}\quad s^{k}=x^{k+1}-x^{k}$Posso procedere con$|s^{k}|<\text{toll}$$

\[\begin{align*}=\frac{1}{1-L}\|s^{k}\|\end{align*}\]

Usiamo un contatore k < n che

Soluzione di sistemi sovra-determinanti

$A\in M_{n\times m}\quad b\in\mathbb{R^n}\qquad\boxed{m>n}$ Trova $k\in\mathbb{R}^{n}:\quad Ax=b$

Ipotesi: RANGO DI A MASSIMO cioè $m$, ovvero le colonne di A sono linearmente indipendenti ($\sum\limits A_{ij}c_{j}=0\ \forall i\quad\Rightarrow\quad c=0$)

Allora $Ax=b$ ha soluzione se e solo se $\begin{align*}b\in\ &\text{span}\{A(,1);A(,2);…;A(,n)\}\\&\searrow\text{spazio limitato generato}\\&=\text{immagine di A }Im(A)\end{align*}$

Trovare una generalizzazione del concetto di soluzione. Lo facciamo considerando la norma $\begin{align*}F:\mathbb{R}^{n}&\rightarrow\mathbb{R}\\ x&\mapsto\|Ax-b\|_{2}^{2}\end{align*}$ e CERCANDO I MINIMI

Osservazione. Se $b\in Im(A)$ allora $\exists!x^{x}$ tale che $Ax=b$ dove $x^{x}$ è soluzione di MQ (minimi quadrati). Infatti la soluzione di MQ se esiste richiama la SOLUZIONE DEI MINIMI QUADRATI

Teorema “caso particolare del problema delle proiezioni ortogonali” Sia $A\in M_{n\times m}(\mathbb{R})\quad m>m\quad rk(A)=n$ $b\in\mathbb{R}^m$ e denotiamo con $F:\mathbb{R}^{n}\rightarrow\mathbb{R},\quad \|Ax-b\|_{2}^{2}$ Allora $\exists!x^{x}\in\mathbb{R}^{n}$ tale che $F(x^{x})=\min_{x\in\mathbb{R}^{n}}$, inoltre $x^{x}$ è caratterizzato dalle EQUAZIONI INTERNE $A^{T}Ax^{x}-A^{T}x$

F è convessa
Se la derivata di una funzione convessa si ammette in un punto, allora quel punto è di MINIMO
Pongo derivata = 0 e cerco di risolverla

DIM: definiamo $f_{v,x}(t):F(x+tv)\quad\forall v\neq0$ $\begin{align*}f_{v,x}:\mathbb{R}&\rightarrow\mathbb{R}\\ t&\mapsto F(x+tv)\end{align*}$ come è fatta $f_{v,x}(\cdot)$ fissati v,x? $\begin{align*}f_{v,x}&=\|A(x+tv)-b\|_{2}^{2}=[A(x+tv)-b]^{T}[A(x+tv)-b]\\&=[x+tv]^{T}A^{T}A(x+tv)=(x+tv)^{T}A^{T}b-b^{T}A(x+tv)+\|b\|_{2}^{2}\\&=x^{T}A^{T}A(x+tv)+tv^{T}A^{T}A(x+tv)-x^{T}A^{T}b-tv^{T}A^{T}b\\&=t^{T}v^{T}A^{T}Av+t[v^{T}A^{T}Av+v^{T}A^{T}Ax-v^{T}A^{T}b-b^{T}Av]+x^{T}A^{T}Ax-x^{T}A^{T}b-b^{T}Ax+\|b\|_{2}^{2}\end{align*}$ è un POLINOMIO DI GRADO 2 in t è una PARABOLA! $\qquad c_{2}t^{2}+c_{1}t+c_{0}$ $c_{2}=v^{T}A^{T}Av=\|Av\|_{2}^{2}\geq0$ $c_{2}>0\quad \bigcup\Rightarrow$ se ammettono le derivate troviamo un minimo

$f_{v,x}^{’}(t)=2tv^{T}A^{T}Av+2x^{T}A^{T}Av-2v^{T}A^{T}t$ ESISTE UN $t^{*}$ che realizza il minimo di $f_{v,x}(\cdot)$ VARIA CON x,v mi accorgo che se prendo $x=x^{*}$ SOL Q. NORMALI $f_{v,x}^{’}(t)=2tv^{T}A^{T}Av+2v(x^{T}A^{T}Av-v^{T}A^{T}t)$ dunque $f_{v,x^{*}}(0)<f_{v,x^{*}}(t)\quad\forall t\in\mathbb{R},\forall v\in\mathbb{R}^{n}/\{0\}$ $F(x^{*}+)$ Dunque se $x^{*}$ risolve le equazioni normali minimizza $F$ su $\mathbb{R}^n$ Ma esiste una soluzione di $A^{T}Ax=A^{T}b$? Sì e dipende dall’ipotesi $A^{T}A$ è simmetrica $\Rightarrow A^{T}A=U^{T}\Lambda U$ $U$ ortogonale $\Lambda$ diagonale con autovalori sulla diagonale

Se $\lambda=0$ fissa autovalore ovvero $A^{T}Ax=0$ con x autovettore $x^{T}A^{T}Ax=\|Ax\|_{2}^{2}\neq0\Rightarrow Ax\neq0$ e l’ipotesi di rango pieno complica $x=0$ quindi x non è autovettore $\Rightarrow\lambda\neq0$ $A^{T}A$ ha autovettori $\neq0$ ()

Possibili soluzioni 1) costruisco $A^{T}A$ e $A^{T}b$ e risolvo il sistema lineare con uno dei metodi già visti NB. $\dim(A^{T}A)=n\times m$ 2) Metodo QR Se $A\in M_{m\times n}\text{ con }m>n\quad rk(A)=n$ esiste la sua fattorizzazione QR - QR = A - $Q\in M_{m\times m}$ ortogonale - $R\in M_{m\times n}$ triangolare superiore $A=Q R=[Q_{0},Q_{1}][{R_{0}\atop0}]=Q_{0}R_{0}+Q_{1}0$ $rk(R)=rk(A)=n$ $R_{0}$ è invertibile SOL EQ NORMALI CON QR 1. $A^{T}Ax^{*}=A^{T}b$ $A^{T}A=\underset{\mathbb{1}_{n}}{\cancel{R^{T}Q^{T}QR}}=R_{0}^{T}Q_{0}^{T}Q_{0}R_{0}$ ATTENZIONE: $\begin{align*}Q_{0}^{T}Q_{0}&=\mathbb{1}_{n}\\ Q_{0}Q_{0}^{T}&\neq\mathbb{1}_{m}\end{align*}$ perché $Q_{0}$ è Q RITAGLIATO 1. $A^{T}b=R^{T}Q^{T}b=R_{0}^{T}Q_{0}^{T}b$ usando 1. e 2. le EQ. NORMALI diventato $R_{0}^{T}R_{0}x^{*}=R_{0}^{T}Q_{0}^{T}b$ $R_{0}$ è invertibile, il sistema di semplifica $R_{0}x^{*}=Q_{0}^{T}b$ triangolare superiore si risolve con sostituzione all’indietro

Cosa c’è di meglio e di peggio nel metodo QR?

Potenzialmente QR è più pesante (m»n)
QR è molto più accurato Se risolviamo $A^{T}Ax^{*}=A^{T}b$ quello che conta è il Cond($A^{T}A,\|\cdot\|$) Se risolviamo $R_{0}x^{*}=Q_{0}^{T}b$ conta Cond($R_0,\|\cdot\|$) $\|A^{T}A\|=\|R_{0}^{T}R_{0}\|\leq\|R_{0}^{T}\|\|R_0\|$ $\|(A^{T}A)^{-1}\|=\|R_{0}^{-1}R_{0}\|$ Sperimentalmente si ha $\begin{align*}Cond(A^{T}A,\|\cdot\|)&\simeq Cond(R_{0}^{T},\|\cdot\|)Cond(R_{0},\|\cdot\|)\\&\simeq[Cond(R_{0},\|\cdot\|)]\end{align*}$ dunque se $Cond(R_{0},\|\cdot\|)$

Zeri di funzioni

Problema: data $f:[a,b]\rightarrow\mathbb{R}$ continua. Trovare $x^{*}\in[a,b]$ tale che $f(x^{*})=0$.

($\exists$) Esiste un tale $x^{*}$? (! ) È unico?

Ad esempio: ($\exists$) Teorema dei zeri: Se $f(a)f(b)<0$ allora $\exists x^{*}\in[a,b]$ con $f(x^{*})=0$ QUESTA È SOLO CONDIZIONE SUFFICIENTE!! (! ) Se $f$ è monotona $\Rightarrow x^{*}$ se esiste è unico. QUESTA È UNA CONDIZIONE SUFF. NON NECESSARIA!! Insomma non è un problema semplice…

IDEA “Metodo di bisezione” Il teorema degli zeri ci fornisce un metodo numerico $\begin{align*}{a_{0}=a\atop b_{0}=b}\quad a_{k+1}&\begin{cases}a_{k}&\text{se }f(a_{k})f(\frac{a_{k}+b_{k}}{2})\leq0\\\frac{a_{k}+b_{k}}{2}&\text{altrimenti}\end{cases}\\ b_{k+1}&\begin{cases}\frac{a_{k}+b_{k}}{2}&\text{se }f(a_{k})f(\frac{a_{k}+b_{k}}{2})\leq0\\ b_{k}&\text{altrimenti}\end{cases}\end{align*}$

$a_{k}$ è SUCC. CRESCENTE! Limitata da sopra $a_{k}<b$ $b_k$ è SUCC. DECRESCENTE! Limitata da sotto $b_{k}>a$ Dunque $\begin{align*}\{Q_{k}\}_{x\in\mathbb{N}}\text{ ha limite }x_{1}\\\{b_{k}\}_{x\in\mathbb{N}}\text{ ha limite }x_{2}\end{align*}$ $|a^{k+1}-b^{k+1}|=\frac{1}{2}|a^{k}-b^{k}|=\frac{1}{2}\cdot\frac{1}{2}|a^{k-1}-b^{k-1}|…$

Quindi $x_{1}=x_{2}$ lo chiamo $x^{*}$

CONDIZIONAMENTO?? Osservazione: Il dato del problema è “$f$” $\mathcal{C}([a,b]):=$ funzioni continue in $[a,b]\in\mathbb{R}$ Proposizione: $\mathcal{C}([e_{i}])$ è spazio vettoriale $f,g\in\mathcal{C}([a,b])\qquad\alpha f\quad\alpha\in\mathbb{R}\quad$ Sappiamo fare le moltiplicazioni (per $\alpha\in\mathbb{R}$) $\begin{align*}f+g:[a,b]&\rightarrow\mathbb{R}\\ x&\mapsto\end{align*}$ Su $\mathcal{C}^{0}([a,b])$ possiamo mettere molte norme, la più importante dei quali è la NORMA UNIFORME. $\displaystyle\|f\|_{x}:=\sup_{k\in[a,b]}|f(x)|=\max_{x\in[a,b]}|f(x)|$ Verifichiamo 1) $\|\lambda f\|$ 2) $\|\lambda f\|_{x}=\sup\limits_{x\in[a,b]}|f(\lambda f)|\geq0$ $\|f\|_{x}=0\Rightarrow\sup_{x\in[a,b]}|f()|=0$ Osservazione: supponiamo che $\|f-g\|_{n}<\varepsilon$

Se $f_{n}$ è una successione di funzioni $f_{n}:[a,b]\longrightarrow\mathbb{R}\quad\forall n\in\mathbb{N}$ Se $\lim\limits_{n\rightarrow+\infty}\|f_{n}-f\|_{n}=0$ si dice che $f_{n}$ TENDE A $f$ UNIFORMEMENTE. Osservazione: Se $f_{n}\rightarrow f$ uniformente $\Rightarrow f_{n}(x)\rightarrow f(x)\quad\forall x\in[a,b]$ ma non il viceversa.

Proposizione: Se $f_{n}\in\mathcal{C}^{0}([a,b])\quad f_{n}$ converge uniformentente e $f:[a,b]\rightarrow\mathbb{R}$, allora $f$ è continua

Condizionamento delle radici di $f$

Supponiamo che $\tilde{f}:[a,b]\rightarrow\mathbb{R}$ e $\|\tilde{f}-f\|_{n}<\varepsilon$ $x^{}\in[a,b]\text{ t.c. }f(x^{})=0\tilde{x}\in[a,b]\text{ t.c. }\tilde{f}(\tilde{x})=0\begin{align}f(\tilde{x})=|f(\tilde{x})-\underset{=0}{\tilde{f}(\tilde{x})}|\leq&\sup_{x\in[a,b]}|f(x)-\tilde{f}(x)|\&=|f-\tilde{f}|_n<\varepsilon\end{align}$Supponiamo che$f\in\mathcal{C}^{1}([a,b])f(\tilde{x})=f(x^{*})+f^{’}(\xi)()$$

$\xi\in\overline{\tilde{x}x^*}$ $|\tilde{x}-x^{*}|\leq\|f-\tilde{f}\|_{n}\cdot\frac{1}{|f^{’}(\xi)|}$ Se $f’\neq0$ allora $f’(\xi)\neq0$ in un intorno I di $x^{*}$, dunque per $\tilde{x}$ sufficientemente vicina a $x^{*}$ abbiamo$$\boxed{\begin{align*}err_{ass}(\tilde{x})\leq C\ err_{ass}(\tilde{f})\\ C=\frac{1}{\min_{I}|f^{’}|}\end{align*}}$ Esempio. $f(x)=Ax+B\qquad A\neq0,B\in\mathbb{R}$ $\tilde{f}(x)=Ax+B+\varepsilon\qquad\varepsilon>0$ $\displaystyle\|f-\tilde{f}\|_{u}=\sup_{x\in[a,b]}|Ax+B-(Ax+B+\varepsilon)|=\varepsilon$ $\displaystyle x^{*}=\frac{-B}{A}\quad\tilde{x}=\frac{-(B+\varepsilon)}{A}\qquad|x^{*}-\tilde{x}|=\left|\frac{-\varepsilon}{A}\right|=\frac{\varepsilon}{|A|}=\underbrace{\frac{1}{|A|}}_{\frac{1}{f’(x)}}\cdot\underbrace{\varepsilon}_{\|f-\tilde{f}\|_{k}}$ ![[IMG_8484.jpeg|IMG_8484.jpeg]] CASO LIMITE se $f’(x^{*})=0$ Abbiamo comunque $(*)\quad|f(\tilde{x})|\leq\|f-\tilde{f}\|_{u}$ $f(\tilde{x})=\underset{=0}{f(x^{*})}+\underset{=0}{f’(x^{*})}(\tilde{x}-x^{*})+\dfrac{f^{”}(\xi)}{2}(\tilde{x}-x^{*})^{2}\quad$ $\displaystyle(\tilde{x}-x^{*})^{2}=\left|\frac{2f(\tilde{x})}{f^{”}(\xi)}\right|\leq\frac{2}{|f^{”}(\xi)|}\|f-\tilde{f}\|_{n}$ $|\tilde{x}-x^{*}|\leq\sqrt{\dfrac{2}{f^{”}(\xi)}}\sqrt{\|f-\tilde{f}\|_{u}}$ IN QUESTO CASO $err_{ass}(\tilde{x})$ è PROPORZIONALE $A=\sqrt{\|f-\tilde{f}\|_{k}}\quad\text{cioè }\sqrt{\varepsilon}>>\varepsilon$

Def. “Molteplicità di una radice” $f:[a,b]\rightarrow\mathbb{R}\qquad f\in\mathcal{C}^{k}([a,b])\quad k\in\mathbb{N}$ $\begin{align}x^{}\in[a,b]\text{ t.c.}\ &f(x^{})=f’(x^{})=…f^{(k-1)}(x^{})=0\&f^{()}(x^{})\neq0\end{align}x^{}$ha molteplicità k Se$x^{}$ ha molteplicità 1 si dice RADICE SEMPLICE. $x^{*}$ radice semplice $\begin{cases}|f’(x’’)|>>0&\text{BEN CONDIZIONATA}\\ |f’(x’’)|\approx0&\text{MAL CONDIZIONATA}\end{cases}$ (funzione pendente, ben condizionata; funzione piatta, mal condizionata)

BISEZIONE Bisezione ha limitazioni (FORTI)

se $f$ conta segno, non si può applicare
se su può applicare, converge ma non è velocissima

Metodo di NEWTON $\begin{cases}x_{0}\quad\text{dato}\\ x_{k+1}=x_{k}-\dfrac{f(x_{k})}{f’(x_{k})}\end{cases}$ Teorema “Convergenza locale per radici semplici” $f\in\mathcal{C}^{2}([a,b])\quad x^{*}$ radice semplice di $f\in[a,b]$, allora esiste un intorno I di $x^{*}$ tale che il metodo di Newton inizializzato con $x_{0}\in I$ converge a $x^{*}$. Inoltre si ha$\lim_{k\rightarrow+\infty}\frac{|e_{k+1}|}{|e_{k-1}|^{2}}=\left|\frac{f’’(x^{*})}{2f’(x^{*})}\right|$DIM Convergenza locale Newton delle radici semplici $0=f(x^{*})=f(x_{k})+f’(x_{k})(x^{*}-x_{k})+\dfrac{f’’(\tilde{\xi})}{2}(x^{*}-x_{k})^{2}$ $x_{k+1}=x_{k}-\frac{f(x_{k})}{f’(x_{k})}\quad$ def. del metodo $\xi_x\in\overline{x^{*}x_{k}}$

Se $f’(x_{k})\neq0$ $\displaystyle0=\underbrace{\frac{f(x_{k})}{f’(x_{k})}+x^{*}-x_{k}}_{=x^{*}-x_{k+1}}+\frac{f’’(\xi)}{2f’(x_{k})}(x^{*}-x_{k})^{2}$ $x_{k+1}-x^{*}=\frac{f’’(\xi)}{2f(x_{k})}(x^{*}-x_{k})^{2}\qquad e_{k}:=x_{k}-x^{*}$ ERRORE CON SEGNO

\[|e_{k+1}|=\frac{}{}|e_{k}|^{2}=\frac{f’’()}{2f’(x_{k})}|e_{k}||e_{k}|\quad(\triangle)\]

Se scelgo $I=[x^{*}-\delta,x^{*}+\delta]$ in modo che $(\square)\qquad\dfrac{f’’(\xi_{k})}{f’(x)}|x-x^{*}|\leq1\quad\forall x\in[x^{*}-\delta,x^{*}+\delta]$ e se $x_{k}\in I$, allora usando $(\triangle)$, ho $|x^{*}-x_{k}|\leq\frac{1}{2}\cdot1|x^{*}-x_{k}|$ Dunque $x_{k+1}\in I$ e posso iterare questo procedimento: se $x_{0}\in I\text{ e se }f’(x_{k})\neq0\quad\forall x\in\mathbb{N}$ $|x^{*}-x_{k}|<\dfrac{1}{2^{k}}|e_{0}|\longrightarrow0$ Vogliamo ora vedere che posizione soddisfa $(\square)$ $x^{*}$ è radice semplice $\begin{align}f(x^{*})=0\\ f'(x^{*})\neq0\end{align}$ dunque prendendo $\delta>0$ sufficientemente piccolo posso assumere che $f’(x)\neq0\quad\forall x\in I$$\displaystyle\frac{f’’(\xi_{k})}{f’(x_{k})}|x-x^*|\quad\leq\frac{f’’(\xi_{k})}{\min_{I}|f’|}\delta\quad\leq\underbrace{\frac{\min_I|f’’|}{\min_{I}|f’|}}_{\text{funz. continua di }\delta}\delta\quad\xrightarrow[\text{se }\delta\rightarrow0]{}0$dunque $(\square)$ è vera per $\delta>0$ sufficientemente piccolo.

Usando $(\triangle)\qquad\displaystyle\frac{|e_{k+1}|}{|e_{k}|^{2}}=\frac{|f’’(\xi)|}{2|f’(x_{k})|}$ osserviamo che da $\quad|e_{k}|\leq2^{-k}|e_{0}|\longrightarrow0$ dunque $x_{k}\rightarrow x^{*}$ ma $\xi_{k}\in\overline{x_{k}x^{*}}$ dunque anche $\xi_{k}\rightarrow x^{*}$ $f\in\mathcal{C}^2$ quindi $f’’\text{ e }f’$ sono continue e dunque $\lim_{k\rightarrow+\infty}\frac{|e_{k+1}|}{|e_{k}|^{2}}=\lim_{k\rightarrow+\infty}\frac{f’’(\xi_{k})}{2|f’(x_{k})|}=\frac{|f’’(x^{*})|}{2|f’(x^{*})|}$(incredibilmente più veloce di bisezione)

FINE PRIMO COMPITINO - - -

La policy “fermarsi alla prima iterazione per cui $\underbrace{|f(x_{k})<toll|}_{\text{test del residuo}}$” sia una buona idea? No, funzioni mal condizionate (funzione piatta) o multiple possono dare valori molti piccoli anche con valori molto distanti.

Criterio di arresto dello scarto (step)

$S_{k}=x_{k+1}-x_{k}$ mi fermo alla prima iterazione per la quale $|S_{k}|<toll$ Vediamo che $|S_{k}|=$ In particolare se $|f'(x)|\approx|f'(x^{*})|$$|f(x_{k})|\leq toll|f'(x^{*})|$possiamo pensare questo criterio come il criterio della derivata PIU IN DETTAGLIO $\begin{align*}f(x_{k})&=f(x)+f'(x)(x_{k+1}-x_{k})+\frac{f''(\xi_{k})}{2}(x_{k+1}-x_{k})^{2}\\&=\frac{f''(\xi_{k})}{2}S_{k}\end{align*}$ $f(x_{k+1})=$

$|e_{k+1}|=\dfrac{|f''(\xi_{k})|}{2|f'()|}|S_{k}|^{2}$ se $x\rightarrow+\infty$ $|e_{k+1}|=\dfrac{|f''(\xi_{k})|}{2|f'()|}|S_{k}|^{2}:=\dfrac{|f''(x^{*})|}{2|f'(x^{*})|}|S_{k}|^{2}$

e_{k+1}

S_{k}

^{2}$$ se con

MORALE: Newton si implementa con ciclo while e test di uscita:

criterio dello step
non massimo di n iterazioni

Osservazione: Newton è uno schema iterattivo $f:[a,b]\rightarrow\mathbb{R}\qquad g(x)=x-\dfrac{f(x)}{f'(x)}$ MAPPA DI IT. DI NEWTON dominio di g è ${x\in[a,b]\text{ t.c. } f’(x)\neq0}$se$x^{}\in[\tilde{a},\tilde{b}]\text{ t.c. }$se$x^{}$tale che$f(x^{*})$$ allora

lemma delle contrazioni da ($\underbrace{[a,b]}_{\neq\mathbb{R}}\rightarrow\mathbb{R}$) $g:[a,b]\rightarrow\mathbb{R}$ tale che

\[g([a,b])\subseteq[a,b]\]

$$\exists L$ Allora

$\exists!x^{}\in[a,b]\text{ t.c. }g(x^{})=x^{*}$
$\forall x_{k}\in[a,b]$ ha tutte le

se $g'(x^{*})\neq0(\text{e }q\in\mathcal{C}')$ allora $$\lim_{x\rightarrow+\infty}\frac{

x_{k+1}-x^{*}

}{

x_{k}-x^{*}

}$$

Cosa succede se $x^{*}$ non è semplice? $g(x)=\begin{cases}x-\frac{f(x)}{g(x)}&x\neq x^{*}\\ x^{*}&x=x^{*}\end{cases}$ supponiamo che $f\leq\mathcal{C}^{2}([a,b])\quad f'(x)\neq0\quad\forall x\in[a,b]$

$g\in\mathcal{C}'$ se $x\neq x^{*}$ $g'(x)=1-\frac{}{}$

MORALE: Newton per radici di molteplicità >1 ha ancora convergenza locale ma perde la convergenza quadratica e $\lim_{}=\frac{1}{2}$

A volte si può conoscere la molteplicità di una radice dalla specifica applicazione pratica; in questo caso possiamo usare il Metodo di Newton Modificato. $x_{k+1}=x_{k}-$

Metodo della secante e metodi “Newton Light” Se non sappiamo scrivere $f'$ o costa troppo, approssimiamo usando metodi del tipo$x_{k+1}=x_{k}-\frac{f(x_{k})}{p_{k}}\qquad p_{k}\approx f'(x_{0})$

$p_{k}=f'(x_{0})$ metodo della tangente fissa
$p_{k}=\frac{f(x_{k})-f(x_{0})}{x_{k}-x_{0}}$ metodo delle secanti variabili

Interpolazione dati e funzioni

$x\longrightarrow f(x)$ e dispongo di “misurazioni” $(x_{i}\quad f(x_{i})=y_{i})\quad i=0,1,…,n$Vogliamo costruire un modello del fenomeno$$x\longrightarrow g(x)$$

facile da costruire
$g$ semplice bella forma e nel caso dobbiamo farci delle operazioni
- integrali
- derivate
- operazioni algebriche
- calcolare massimi, minimi, etc $If$ interpola i dati $(x_{i},y_{i})\quad i=0,1,…,n$se$g(x_{i})=y_{i}\quad\forall i=0,1,…,n$Potrebbe darsi che invece$f:[a,b]\rightarrow\mathbb{R}$sia una funzione nota o calcolabile ma molto complessa, in tal caso si può voler produrre$g:[a,b]\rightarrow\mathbb{R}\quad\text{tale che }g\approx f$In un senso OPPORTUNO, ad esempio$|f-g|_{x}2\text{toll}$$

$g$ si dice modello surrogato, e può essere costruito per interpolazione cioè $g(x_{i})=f(x_{i})\quad i=0,1,...,n$

Considero $\phi_{1},\phi_{2},...,\phi_{n}\in\mathcal{C}^{0}([a,b])$ $\Phi:=\text{span}(\phi_{1},\phi_{2},...,\phi_{n})$ span = spazio lineare generato $\phi\in\Phi\qquad\phi(x)=\sum\limits_{j=0}^{n}c_{j}\phi_{j}(x)\quad c_{j}\in\mathbb{R}$ $\phi,\psi\in\Phi\qquad\phi(x)$ $\sum\limits c_{j}\phi_{j}\sum\limits b_{j}\phi_{j}\qquad\lambda\phi(x)=\sum\limits_{j}\lambda c_{j}\phi_{j}(x)$ dunque è spazio vettoriale $X=\{x_{0},x_{1},...,x_{n}\}\quad x_{i}\in[a,b]$ cerchiamo $\phi\in\Phi\ :\ \phi(x_{i})=y_{i}\quad\forall i=0,1,...,n$ se una tale $\phi$ esiste, è un interpolante dei dati $(x_{i},y_{i})\ i=0,1,...,n$$\phi(x_{i})=\sum\limits_{j=0}^{n}c_{j}\phi_{j}(x_{i})\underset{\text{cond. interpolazione}}{=}y_{i}\qquad i=0,1,…,n$$Ac=y\qquad A_{ij}$ La matrice $A=(\phi_{j}(x_{i}))_{i=0,...,n}$ è detta matrice di Vandermonde Esempi fondamentali: 1) interpolazione algebrica $\phi_{j}(x):=x^{j}$ $\Phi=\text{span}\{1,x,x^{2},...,x^{n}\}$ polinomi di grado $\leq n$ $A=\begin{matrix}1&x_{0}&x_{0}^{2}&...&x_{0}^{n}\\1&x_{1}&x_{1}^{2}&...&x_{1}^{n}\\\vdots\\1&x_{m}&x_{m}^{2}&...&x_{m}^{n}\end{matrix}\begin{align}\text{grado}\leq n&\rightarrow n+1\text{colonne}\\\end{align}$ 2) interpolazione trigonometrica (numerazione da -n a n) $\phi_{j}(x)=e^{inx}=\cos(nx)+i\sin(nx)$ caratteri di Fourier Per fenomeni periodici $[0,2\pi]\rightarrow\mathbb{S}^{2}$ Osservazione: se A è quadrata e invertibile allora $A^{-1}y$ è l’unica soluzione del sistema di Vandermonde $Ac=y$$\phi(x)=\sum\limits_{j=0}^{n}(A^{-1}y){j}\phi{j}(x)$$se m>n e le collonne di A sono limitate indipendentemente esiste soluzione solo se $y\in\text{span}(A_{i0},A_{i1},…,A_{in})$ e in tal caso è UNICA.

TEOREMA: Nel caso algebrico ($\phi_{j}(x)=x^{j}\ j=0,1,…,n$) e con m=n, allora la matrice di Vandermonde è invertibile <u>se e solo se</u>$x_{i}\neq x_{j}\quad\forall i\neq j$$

Dimostrazione: m=n $A=\begin{matrix}1&x_{0}&x_{0}^{2}&...&x_{0}^{n}\\1&x_{1}&x_{1}^{2}&...&x_{1}^{n}\\\vdots\\1&x_{m}&x_{m}^{2}&...&x_{m}^{n}\end{matrix}$ Tolgo ad ogni colonna tranne la prima, la precedente moltiplicata per $x_{0}$. Questa operazione corrisponde alla moltiplicazione per matrice triangolare superiore con 1 sulla diagonale U. $\det(AU)=\det A\cdot\det U=\det A\cdot1\cdot1\cdot...\cdot1$ dunque non cambia il determinante. $\det\left[\begin{array}{c|cccc}1&0&0&...&0\\\hline1&x_{1}-x_{0}&x_{1}^{2}-x_{1}x_{0}&...&x_{1}^{n}-x_{1}^{n-1}x_{0}\\\vdots\\1&x_{m}-x_{0}&x_{m}^{2}-x_{n}x_{0}&...&x_{m}^{n}-x_{n}^{n-1}x_{0}\end{array}\right]=\begin{bmatrix}(x_{1})1&0&0&...&0\\1&x_{1}-x_{0}&x_{1}^{2}-x_{1}x_{0}&...&x_{1}^{n}-x_{1}^{n-1}x_{0}\\\vdots\\1&x_{m}-x_{0}&x_{m}^{2}-x_{n}x_{0}&...&x_{m}^{n}-x_{n}^{n-1}x_{0}\end{bmatrix}$ $\det\begin{bmatrix}(x_{1}-x_{0})&0&&&\\0&(x_{2}-x_{0})&0&--&\\\vdots\\0&&&...&(x_{m}-x_{0})\end{bmatrix}$

$\prod_{i_{1}=1}^{n}(x_{i_{1}}-x_{0})\cdot\prod_{i_{1}=0}$

se $x_{i}\neq x_{j}\quad\forall i\neq j$ allora $\det A$ è il prodotto di termini non nulli $\Rightarrow\det A\neq0$ A invertibile
se $\det A=0\Rightarrow$ almeno uno dei fattori deve essere nullo e dunque $x_{i}=x_{j}$ per almeno una coppia di indici $(i,j)\quad i\neq j$

Morale: se prendiamo punti distinti di grado max+1 la Vandermonde è invertibile e $\exists!$ polinomio interpolante $p\in\mathcal{P}^{n}$ Tale che $p(x_{i})=y$

Polinomi di Lagrange (FLIPS) Supponiamo di avere a disposizione $\ell_{0}(x),\ell_{1}(x),...,\ell_{n}(x)$ Tali che $\ell_{j}(x_{i})=\delta_{ij}:=\begin{cases}1&\text{se }i=j\\1&\text{se }i\neq j\end{cases}\quad$ con $\ell_{j}\in\Phi$ Allora $\phi\in\Phi$ tale che $\phi(x_{i})=y_{i}$ si scrive $\phi(x)=\sum\limits_{i=0}^{n}y_{i}\ell_{i}(x)$ $\phi(x_{k})=\sum\limits_{i=0}^{n}y_{i}\underbrace{\ell_{i}(x_{k})}_{0\text{ se }i\neq k\text{ o 1 se}i=k}=y_{k}\ell_{k}(x_)$ Se dispongo dei $\ell_{i}$ il problema dell'interpolazione è risolta. Ma è vero che esistono gli $\ell_{i}\quad i=0,1,...,n$ (base di Lagrande)?

se A è invertibile, la base di Lagrange esiste ed è unica! $\ell_{k}(x)\underset{\text{elem di }\Phi}{=}\sum\limits_{j}c_{j,k}\phi_{j}(x)$ $\ell_{k}(x_{0})=\sum\limits_{j}c_{j,k}\phi_{j}(x_{0})=0$ $\ell_{k}(x_{1})=\sum\limits_{j}c_{j,k}\phi_{j}(x_{1})=0$ $\ell_{k}(x_{0})=\sum\limits_{j}c_{j,k}\phi_{j}(x_{i})=0$ $\vdots$ $\ell_{k}(x_{k})=\sum\limits_{j}c_{j,k}\phi_{j}(x_{k})=1$ $c_{j,k}:=\begin{bmatrix}c_{0,k}\\ c_{1,k}\\\vdots\\c_{n,k}\end{bmatrix}$ ma allora $A[c_{j,0},c_{j,1},...,c_{j,n}]=[]$ quindi $c_{j,k}$ è la k-esima colonna di $A^{-1}$ se consideriamo il caso algebrico, la base di Lagrange è detta dei polinomio di Lagrange

“Incredibilmente” abbiamo una formula esplicita $\ell_{j}$ è un polinomio che si annulla su ogni $x_{i}$ con $i\neq j$ cioè n punti $\ell_{j}$ è di grado $\leq n$ $\prod_{i\neq j}\frac{\ell_{j}(x)}{x-x_{i}}=$ costante perché è polinomio di grado 0 $\frac{\ell_{j}(x_{i})}{\prod_{j\neq i}x_{j}-x_{i}}=\frac{1}{\prod_{j\neq i}x_{j}-x_{i}}$ $\ell_{j}(x)=\frac{\prod_{j\neq i}x-x_{i}}{\prod_{j\neq i}x_{j}-x_{i}}$

Le colonne di $V^{-1}$ sono i coefficienti del polinomio di Lagrange $\ell_{0}(x),\ell_{1}(x),...,\ell_{n}(x)$ che sono gli unici polinomi che soddisfano $\ell_{j}(x_{i})=\delta_{ij}:=\begin{cases}1&\text{se }i=j\\1&\text{se }i\neq j\end{cases}$

Com’è condizionato (termini assoluti) il problema dell’interpolazione? $f:\mathcal{C}^{0}([a,b])\text{ e }\tilde{f}\in\mathcal{C}^{0}([a,b])$ sia approssimazione in NORMA UNIFORME $\|f\cdot\tilde{f}\|_{n}=\max_{x\in[a,b]}|f(x)-\tilde{f}(x)|$ p polinomio che interpola $f\text{ in }x_{0},x_{1},...,x_{n}$ $p(x_{i})=f(x_{i})$ $\tilde{p}$ polinomio che interpola $\tilde{f}\text{ in }x_{0},x_{1},...,x_{n}$ $\tilde{p}(x_{i})=\tilde{f}(x_{i})\quad\forall i$ Vogliamo una stima di $\|p-\tilde{p}\|_{n}$ $|p(x)-\tilde{p}(x)|=|\sum\limits_{i=0}^{n}f(x_{i})\ell_{i}(x)-\sum\limits_{i=0}^{n}f(x_{i})\ell_{i}(x)|=|\sum\limits_{i=0}^{n}(f(x_{i})-\tilde{f}(x_{i}))\ell_{i}(x)|$ $\begin{align}\|p-\tilde{p}\|_{n}&=\max_{x\in[a,b]}|f(x)-\tilde{f}(x)|=\\&\leq\max_{x\in[a,b]}|\sum\limits_{i=0}^{n}(f(x_{i})-\tilde{f}(x_{i}))\ell_{i}(x)|\end{align}$ dunque $\max_{x\in[a,b]}|f(x)-\tilde{f}(x)||\ell_{i}(x)|\leq\|f-\tilde{f}\|_{n}\max_{x\in[a,b]}|f(x)-\tilde{f}(x)|$ quindi $$\|p-\tilde{p}\|\leq\|f-\tilde{f}\|$ la quantità $\Lambda(x_{0},x_{1},…,x_{n},[a,b]):=\max_{x\in[a,b]}|\ell_{2}(x)|$detta COSTANTE DI LEBESGUE, misura di condizionamento assoluto del problema di interpolazione dipende solo da$[a,b]\text{ e }x_{0},x_{1},…,x_{n}$$

Osservazione: costandi di Lebesgue molto grandi distruggono la qualità dell’interpolazione

necessariamente $\Lambda\rightarrow+\infty\text{ se }n\rightarrow+\infty$ indipendentemente da come scelgo i nodi
la velocità con cui $\Lambda\rightarrow+\infty\text{ se }n\rightarrow+\infty$ dipende da come scelgo i nodi

Domanda importante: sia $f\cdot\mathcal{C}^{0}([a,b])$ e considero $x_{0}^{(n)},x_{1}^{(n)},...,x_{n}^{(n)}$ Cosa succede a $\|f-p_{n}\|_{n}$ dove $p_{n}$ è interpolante di $f\text{ su }x_{0}^{(n)},x_{1}^{(n)},...,x_{n}^{(n)}$? “Vorrei” poter concludere che $p_{n}\rightarrow f$

in realtà nessuno mi assicura che $\underset{\text{se }n\rightarrow+\infty}{\|f-p_{n}\|_{n}\rightarrow0}$ Fissati i nodi di interpolazione per ogni grado posso introdurre l’operatore di interpolazione $$\begin{align}I_{n}:\mathcal{C}^{0}([a.b])&\longrightarrow\mathcal{P}^{n}\\ f&\longmapsto\sum\limits_{i=0}^{n}\ell_{i}(x)f(x_{i}^{(n)})\end{align}$ 1) $I_{n}$ è lineare $I_{n}(af+bg)=aI_{n}(f)+bI_{n}(g)\quad\forall a,b\in\mathbb{R},\ f,g\in\mathcal{C}^{0}([a,b])$ 2) $I_{n}$ è un OPERATORE DI PROIEZIONE DI $\mathcal{P}$ $I_{n}(p)=p\text{ se }p\in\mathcal{P}$ $I_{n}$ è un Vale $p(x_{i}^{(n)})$ in $x_{i}^{(n)}$ per $i=0,1,…,n$ma anche p soddisfa le condizioni$q(x_{i}^{(n)})=0\quad\forall i=0,1,…,n$(Teorema fondamentale dell'algebra) Un polinomio di grado n non identicamente nullo ha esattamente n zeri in$\mathcal{C}$ contati con la loro molteplicità. $\Rightarrow q(x)=0\text{ cioè }I_{n}(q)\sim$

Teorama di approssimazione di Wierstrass se $f\in\mathcal{C}^{0}([a,b])\quad\forall\epsilon>0\ \exists p_{\epsilon}\text{ polinomi tali che }\|f-p_{\epsilon}\|_{n}<\epsilon$ Attenzione: non abbiamo informazioni sul grado di $p_{\epsilon}$
Teorema di Jackson Se $f\in\mathcal{C}^{k}([a,b])\quad b\geq c\text{ allora }\exists c$ $\inf_{p\in\mathcal{P}^{n}}\|f-p\|\leq c\|f^{(k)}\|_{n}n^{-k}$ Attenzione: stiamo misurando l’errore di approssimazione di f con “il migliore polinomio di grado n” possibile Stima di Lebesgue dell’errore di interpolazione $\|f-I_{n}f\|=\|f-p_{n}+p_{n}-I_{n}f\|$ $I:$ interpolante suigli (n+1) nodi scelti sul passo n $p_{n}:$ polinomio di grado n che realizza $\|f-p_{n}\|_{n}=\min_{q\in\mathcal{P}^{n}}\|f-q\|_{n}$ ESISTE DAVVERO! $p_{n}$ è polinomio di miglior approssimazione uniforme $\begin{align}&\leq\|f-p_{n}\|_{n}+\|p_{n}-I_{n}f\|_{n}\\&=\|f-p_{n}\|_{n}+\|I_{n}(p_{n})-I_{n}(f)\|_{n}\\&=\|f-p_{n}\|_{n}+\|I_{n}(p_{n}-f)\|_n\end{align}$ $(I_{n}(p_{n}-f))(x)=\sum\limits_{i=0}^{n}(p_{n}(x_{i}^{(n)})-f(x_{i}^{(n)}))\ell_{i}(x)$ stesso calcolo di prima $\leq\max_{x\in[a,b]}\sum\limits_{i=0}^{n}$ $\begin{align}\|f-I_{n}f\|\leq\|f-p_{n}\|_{n}\leq\end{align}$ Abbiamo spezzato la stima in due fattori
$1+\lambda$ dipende solo dal $[a,b],\ x_{0},x_{1},…,x_{n}$$
$\min_{p\in\mathcal{P}^{n}}\|f-p\|_{n}$ dipende solo da $f$ per esempio, Jackson mi dice che con questo fattore $\rightarrow0\text{ se }f$ è almeno $\mathcal{C}'$ Ci siamo chiesti se $\|f-I_{n}f\|_{n}\rightarrow0\text{ se }n\rightarrow+\infty$ Risposta: dipende da quali nodi scelgo e da quanto “liscia” è $f$

Attenzione: classico esempio di nodi “cattivi” $[a,b]=[-1,1]\quad x_{i}^{n}=$ nodi equispaziati $\Lambda_{n}=\Lambda([-1,1],x_{0}^{n}...x_{i}^{n})\sim e^{n^{2}}$

esempio di nodi “buoni” Nodi di Chebyshev in $[-1,1]$ 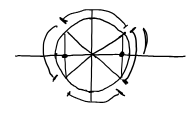![](img/Pasted%20image%2020241202174520.png) punti equispaziati in una circonferenza unitaria proiettati $\displaystyle\cos\left[\frac{\not2\pi}{\not2n}i+\frac{\pi}{2n}\right]\quad i=0,1,...,n$ non contengono gli estremi $$\Lambda_{n}\sim 1+\log n$

Nodi di Chebyshev + Lobatto 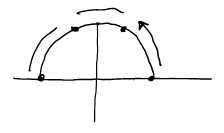$\displaystyle\cos\left(\frac{\pi}{n}i\right)\quad i=0,1,…,n\Lambda_{n}\sim a+\log n\quad a\approx2$$

$x_{0},...,x_{n}$ nodi distinti $y_{0},...,y_{n}$ dati $(y:=f(x_{i}))$ $p(x)=\sum\limits_{y=0}^{n}\ell_{j}(x)y_{i}$ polinomio interpolante

Quello che ci interessa nella pratica è il valore di $\ell$ su punti di valutazione pensiamo di fissare $x_{0}^{eval},x_{1}^{eval},...,x_{n}^{eval}$ $\begin{bmatrix}p(x_{0}^{eval})\\ p(x_{1}^{eval})\\\vdots\\ p(x_{n}^{eval})\end{bmatrix}=\begin{bmatrix}\sum\limits_{j=0}^{n}\ell_{j}(x_{0})\\\sum\limits_{j=0}^{n}\ell_{j}(x_{1})\\\vdots\\\sum\limits_{j=0}^{n}\ell_{j}(x_{n})\end{bmatrix}$ Osservazione: la matrice è di forma $[\ell_{j}(x_{i}^{eval})]_{i=0,...,n\atop j=0,...,m}$ è una matrice di Vandermonde rettangolare rispetto alla base $\ell_{0}(x),...,\ell_{n}(x)$ di $\mathcal{P}^{n}$ e ai punti $x_{0}^{eval},x_{1}^{eval},...,x_{n}^{eval}$ ovviamente NON vale $\ell_{j}(x_{i}^{eval})=\Sigma_{j}$

Come calcolo questa Vandermonde rettangolare

(opzione 1) uso $\ell_{j}(x)=\prod_{i\neq j}^{n}\frac{x-x_{i}}{x_{i}-x_{j}}$
(opzione 2) uso l’altra proprietà dei punti di Lagrange $\ell_{j}(x)=\sum\limits$ quali la V=Vandermonde nella base $x^{0},x^{1},...,x^n$ e relativa $x_{0},x_{1},...,x_{n}$ dunque $\ell_{j}(x_{i}^{eval})=\sum\limits_{=0}(n)$ $\begin{bmatrix}\ell_{j}(x_{0}^{eval})\\\vdots\\\ell_{j}(x_{n}^{eval})\end{bmatrix}=\begin{bmatrix}\sum\limits_{=0}^{n}\ell(x)\end{bmatrix}$ quindi $\boxed{[\ell_{j}(x_{i}^{eval})=]}$ Occhio alla compatibilità dei prodotti

Posso calcolare le colonne di $A^{k}$ una alla vota come soluzioni di $V^{k}x=(V^{eval})_{i,j}^{t}$ $=LU\qquad PV^{k}=LU$ “costa” $O(n^{2})$ $V^{k}x=(V^{eval})_{ij}^{t}$ $\cancel{PV^{k}}x=()$ $y=Ux$ i due passi costano più o meno lo stesso ma il secondo può funzionare in parallelo QR$\qquad V^{k}=QR$

è più stabile
si può “innestare”, se il Cond(V)»1$\qquad V^{k}\approx QR$ uso la R come cambio di base moltiplica a dx per una matrice in V vuol dire sostituire colonna con una lineare delle al

Idea: calcolo 2 volte QR, uso R come precondizionatore, poi risolvo $R^{-1}V^{k}x=y$ euristica “twice is enough” se uso QR 1 volta per precodizionamento a $\ell$ per risolvere uho una esatta a se Cond(V)<$\frac{1}{\epsilon_{MACH}}$

Il mal condizionamento nell’uso della matrice di Vandermonde per interpolazione dipende da

modi di interpolazione
basi scelte per i polinomi Se la van
sono un’eccellente base dal punto di vista numerico
“oscillano” $\max_{[-1,1]}T_{n}x$ tutti i max e i min locali su $T_{n}$ sono con valore 1,1

Rappresentazione dell’errore di interpolazione $f\in\mathcal{C}^{n-1}([a,b])\quad x_{1},...,x_{n}$ nodi distinti $E_{n}f(x):=f(x)-g(x)$, dove $p\in\mathcal{P}^{n}$ che interpola $f\text{ su }x_{0},...,x_{n}$ Allora $$\forall x\in[a,b]\exists$

… lezioni da aggiungere … (09/12/2024)

Quadratura numerica

$[a,b]\subset\mathbb{R}\qquad f\in\mathcal{C}^{0}([a,b])$ $\int_{a}^{b}f(x)dx=?\qquad\simeq\sum\limits_{i=a}^{b}f(i)dx$ quadratura $\begin{rcases}I(f,[a,b])=\int_{a}^{b}f(x)dx\\ Q_{x,w}(f)=\sum\limits_{i=a}^{b}f(x)dx\end{rcases}\rightarrow$ sono operazioni lineari su $f$ Formule integratorie $\int_{a}^{b}f(x)dx\approx\int_{a}^{b}p(x)dx$ Idea: facciamo diventare questa una formula di quadratura (interpolatoria) $\begin{align*}I(p,[a,b])&=I(\sum\limits_{i=a}^{b}p[a,b])\\&=\sum\limits_{}^{}I()\end{align*}$ Se uso l’integrale di Lagrange, allora ho $x_{0}=$ $\int_{a}^{b}f(x)dx\approx\int_{a}^{b}p(x)dx=\sum\limits_{a}^{b}p()$ Def: Sia (X,W) una forma di quadratura su $[a,b]$ diciamo che (X,W) ha grado di polinomiale$I(p,[a,b])=Q_{X,W}(\sum\limits_{X}z,\phi)$ $\sum z_{i}I(\phi,[a,b])=\sum\limits zQ_{X,W}(\phi)$ Notiamo che se vale per ogni funzione di base allora vale anche nella forma in cui è scritta $n=I(\phi,[a,b])=Q_{X,W}(\phi)$ è una Vandermonde ma sto quadrando Le formule di grado di esattezza n

se V Vandermonde di grado di quadratura
un punto di quadratura
un vettore di momenti della base tale che $\int_{a}^{b}\phi dx=n$ Formula del trapezio

Cambio variabili, utile per calcolare i pesi $\displaystyle\int_{a}^{b}f(x)dx\underset{}{=}\int_{0}^{1}f(a+(b-a)t)(b-a)dt$ $I(f,[a,b])=(b-a)I(\tilde{f},[0,1])\approx(b-a)\int_{0}^{1}\tilde{f}(t)dt$ con $f$ interpolabile su $\tilde{f}$ $\tilde{f}(x)=\sum\limits_{i=0}^{1}\tilde{f}(x)$ Formula della parabola formule di Newton-Colts, interpolatorie con nodi interspaziati

equispaziati

… In alternativa possiamo vedere che i nodi sono simmetrici

uni-notes

Calcolo numerico

Aritmetica del calcolatore

Sistemi non decimali

Numeri macchina

Stabilità di un algoritmo

Algebra lineare numerica

CONDIZIONAMENTO RELATIVO del problema Ax=b

Metodi per la soluzione di Ax = b

Metodi iterattivi per la soluzione di Ax=b

Soluzione di sistemi sovra-determinanti

Zeri di funzioni

Condizionamento delle radici di \(f\)

Criterio di arresto dello scarto (step)

Interpolazione dati e funzioni

Quadratura numerica